Othello strateegia
Othello reeglid | Othello strateegiaMängi Othellot
Sissejuhatus
Võitja Othellos, nagu juba öeldud, on see mängija, kellel on mängu lõpuks kõige rohkem nuppe laual. Uued mängijad aga tihtipeale kipuvad kasutama seda põhimõtet igal käigul, selle asemel, et kujundada see pikaajaliseks taktikaks. Teisisõnu nad üritavad igat käiku teha nii, et nad saaksid maksimaalse arvu nuppe ümber pöörata. Seda kutsutakse maksimaalsete nuppude strateegiaks (maximum disc strategy). Peale mõningaid mänge kogenud mängijate vastu seda strateegiat kasutades näeb mängija, et see strateegia pole eriti hea strateegia.Maksimaalsete nuppude strateegia
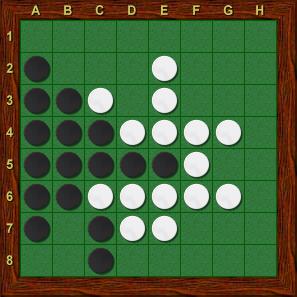
Joonisel 11 on toodud näide, kus mustal on ainult 1 nupp laual, ja 4 ruutu on vabad. Kas see tähendab valge võitu?
Joonis 11: Musta käik.
Must võib käia a1 või h8 (vt. Joonis 11). Sedaviisi peab aga valge mängija kogu aeg oma käigukorra üle andma mustale, kuna tal ei teki võimalust käia. Peale 4 käiku must võidab mängu 40-24! Nagu näha, ei pruugi tulla võit, isegi kui mängijal on palju rohkem nuppe kui vastasel ja mängu lõpuni on väga vähe jäänud. Joonisel 11 on valgel küll palju nuppe, aga nad on haavatavad - neid saab vastane ümber pöörata. Seega on tähtis omada nuppe, mida ei saa vastane mingil juhul ümber pöörata, ükskõik kuidas mäng kulgeb. Selliseid nuppe kutsutakse stabiilseteks nuppudeks (stable discs). Tihtipeale on aga väga raske tekitada stabiilseid nuppe enne mängu lõppfaasi; Järgnevalt mõned näited stabiilsete nuppude kohta.
Stabiilsed nupud – positsiooniline strateegia
On võimatu ümber pöörata nuppu, mis asub nurgas, kuna ta ei saa kunagi jääda kahe vastase nupu vahele. Seega nurgas asuv nupp on alati stabiilne nupp. Lisaks nupud, mis paiknevad nurgas asuva nupu kõrval, on samuti stabiilsed.
Joonis 12: Stabiilsed nupud.
Näiteks joonisel 12 on laual 26 stabiilset nuppu sõltumatult sellest, kus ja kuidas võiksid teised nupud sel laual asetseda. Tulemuseks on see, et mängu lõpuks on mustal mängijal vähemalt 26 nuppu.

Joonis 13: Musta käik.
Joonisel 13 tekitaks must omale 23 stabiilset nuppu, kui ta käiks ruudule h8 (veerud g ja h, read 7 ja 8 ning nupp f6) (vt joonis 14).

Joonis 14: Peale musta käiku: h8.
Must on nüüd seisus kus tal on väga suur võimalus võita see mäng. Nüüd on vaja mängu lõpuks saada veel 10 nuppu ning tal on laual 33 nuppu, mis tagabki võidu.
Seega on Othellos nurgad väga suure tähtsusega: nad võimaldavad saada servadesse veelgi rohkem stabiilseid nuppe. Samas nurgad ei pruugi olla ka alati head (seda käsitleme hiljem). Tasub aga meelde jätta, et nurka tasub vastane lasta vaid siis, kui on paremaid käike millega vastata. Lihtsaim viis vastane mitte nurka lasta on mitte käia nurgaga külgnevale ruudule (X ja C-ruudule). Nii kui üks oma nupp asub ühel nendest kolmest ruudust, on vastasel võimalus seda ära kasutada ja nurka pääseda.
Joonisel 15 on must käinud X-ruudule b7, arvates, et vastane ei saa nurka, kuna diagonaalil pole ühtegi valget nuppu. Valge võib aga käia d8 (vt. Joonis 16), mis pöörab ümber ruudul d5 asuva musta nupu ning lubab tal järgmise käigu ajal hõivata nurk a8. Mustal pole antud juhul mingit võimalust ruudul d5 asuvat valget nuppu tagasi pöörata.

Joonis 15: Valge käik

Joonis 16: Pärast valge käiku d8
Lisaks, tänu isoleeritud mustale nupule b1, on valgel võimalus võtta veel ka teine nurk a1. Kui valge käiks c1 (joonis 16) ähvardades järgmisel käigul käia a1 peale, siis et seda ära hoida, peaks must käima d1, mistõttu saab ümber pöörata ruudul c1 asuva valge nupu. Tänu ruudul e1 asuvale nupule saab aga valge siiski käia ruudule a1. Seega on must teinud väga halva käigu C-ruudule b1. Et olla täpsem: C-ruudule käidud nupu oht on kõige suurem siis, kui ta on teistest nuppudest isoleeritud (isoleeritud = pole ühendatud teiste nuppudega piki mängulaua serva). Näiteks joonisel 13 on mustal alumises paremas piirkonnas hõivatud mõlemad C-ruudud, aga need pole ohtlikud, kuna mustad nupud hõivavad kogu serva.
Kiilud
Me oleme juba näinud, et nurgad on tähtsad. Seega on oluline teada, kuidas tuleb servadesse käia. Vaatleme alumist serva järgmises näites (vt. Joonis 17). Kui must käib c8, siis saab ta järgmise käiguga võtta ruudu a8, vaatamata sellele, mida vastane teeb. C8-l asuvat nuppu ei saa vastane kuidagi tagasi pöörata, kuna ta asub servas ja 2 juba laual oleva valge nupu vahel. Öeldakse, et must nupp on kiilutud.Mis seis on aga idaservas? Kui must käib h6, siis ta nupp pole kiilutud ja vastane saab selle võtta tagasi käies h5 (ja vastupidi kui must käib h5, siis vastane võtab selle tagasi käies h6).
Nüüd vaatleme ülemist serva. Kui must käib c1, siis valge saab selle tagasi võtta käies d1, et vältida vastasel nurka minemast. Siiski saab seejärel must oma nupu kiilutada e1 peale, ja järgmisel käigul saab ta kindlalt võtta nurga a1.
Seega paistab üsna selge, et kui kahe sama värvi nupu vahel on paaritu arv tühje ruute, siis on võimalus vastasel oma nupp sinna vahele kiilutada (nagu joonisel 17 alumises ja ülemises servas), ning kui seal on paaris arv tühje ruute, siis on võimalik kiilutamist ära hoida (nagu joonisel 17 ida servas).

Joonis 17: Musta käik.
Tänu põhimõttele, et tuleks vältida C ja X-ruute, paljud algajad mängijad teevad sellest valesid järeldusi. Nad annavad igale ruudule mingi kindla väärtuse - Teisisõnu: nurgad on alati väga head, servad (v.a. C-ruudud) on ka head, aga mitte nii head, keskmised ruudud on neutraalsed ja X ja C-ruudud on väga halvad. Ja igal käigul nad käivad sinna, mis on eelmainitud järjekorras kõige paremad. Selline strateegia on aga vigane strateegia. Ja nendest põhjustest, miks see nii on, räägime üsna pea.
Mobiilsus
Nagu juba öeldud, et vältida vastasel nurka saamast, tuleks vältida mängimist ruutudele, mis asuvad vahetult nurga kõrval. Sellegipoolest tekib vahest olukord, kus muud võimalust pole. Vaatame joonist 18.
Joonis 18: Musta käik.
Valgel on väga vähe võimalikke käike. Kui must käiks e8, siis jääks valgele vaid 2 käiku: b2 ja g2 (vt. Joonis 19).

Joonis 19: Peale musta käiku e8.
Nüüd on sunnitud valge käima kas b2 või g2. kui see käik on b2, siis saab must nurga a1 ja kui g2, siis saab must nurga h1. Lisaks sellele, kuna ülemises servas on järjestikku 6 nuppu, siis saades ühe nurga, saab järgmisel käigul must omale ka teise nurga.
Selles punktis võime alustada sellega, et kuidas arendada head strateegiat Othellos. Vastane ei käi C- ja X-ruutudele kui tal on võimalus mujale käia. Seega tuleks vastast sundida sinna käima. Et seda saavutada, tuleks vähendada vastase võimalusi käia erinevatesse kohtadesse, nagu oli joonisel 18. Vastasele oli jäetud olukord, kus ta pidi käima X-ruudule ja mustal oli suur eelis mäng võita.
Joonisel 20 on järgmine näide.

Joonis 20: Musta käik.
Kui must käib g6, siis jääb valgele järele vaid 1 käik b2 (vt. Joonis 20). Loomulikult, kuna mustal pole siis ühtegi nuppu diagonaalil b2-e5, siis ei saa ta võtta kohe nurka, aga tal pole mingi probleem see must nupp sinna tekitada. Näiteks kui ta käiks e1, siis pööraks ta ümber valge nupu mis asub ruudul c3 (vt. Joonis 21), ja seda enam valge tagasi pöörata ei saa ja järgmisel käigul on ruut a1 musta mängija käes.

Joonis 21: Mängu seis peale g6-b2-e1.
Joonistel 18 ja 20 on mustal mängijal väga hea mobiilsus, kuna tal on väga palju erinevaid võimalikke (häid) käike, samal ajal valgel on halb mobiilsus, kuna tal on vähe võimalikke keskpäraseid käike.
Üldine reegel on vähendada vastase võimalusi käia, samal ajal enda võimalusi suurendades. Seda kutsutakse mobiilsus-strateegiaks. Kui selle strateegia eesmärk on mängija poolt saavutatud, siis öeldakse, et mängija kontrollib mängu. Kuid peab meeles pidama, et tuleb vastast sundida tegema halba käiku. Sellest ei piisa, kui vastasel on ainult 1 hea käik, tal ei tohi ühtegi head käiku olla.
Piirinupud:
Iga käik tehakse alati tühjale ruudule, vastase nupu kõrvale. See on põhimõte, mis aitab meil valida head käiku.Iga käiguga peab ümber pöörama vähemalt ühe vastase nupu. On selge, et mida rohkem vastase nuppe on tühjade ruutude kõrval, seda rohkem on mängijal käike, seega seda parem on mängija mobiilsus. Vastupidi, kui mängijal on vähe nuppe tühjade ruutude kõrval, siis vastasel on väga vähe võimalikke käike – vastasel on halb mobiilsus. Nuppu, mis asub tühja ruudu kõrval, kutsutakse piirinupuks. Ülejäänusid kutsutakse sisemisteks nuppudeks. Seega, nagu ennist öeldud, tuleks maksimaalselt vähendada oma piirinuppude arvu.
Joonistel 22, 23 ja 24 on kolm üsna sarnast olukorda. Milline seis tekiks, kui must käiks a6 peale kõigis nendes olukordades?

Joonis 22: Kas must tohiks käia a6 ??
Joonisel 22 käik a6 paistab olevat väga halb. Pärast seda, kui valge vastab g1, on must sunnitud andma nurga valgele (kuna mustal on siis ainukesed käigud b1, g2 ja h2). A6 peale mängimine on väga halb, kuna see pöörab ümber suure hulga piirikinuppe (6-ndal real) ja muudab selle rea selliseks, kuhu kõrvale must enam käiku teha ei saa.
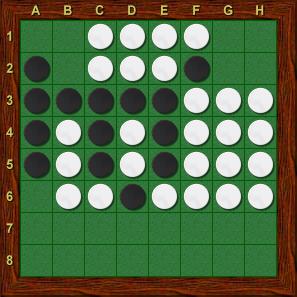
Joonis 23: Kas must tohiks käia a6 ??
Joonisel 23 on a6 peale mängimine mõistlikum kui eelmises näites, kuna ainukesed pööratavad piirinupud on b6 ja c6. Siiski see käik võtaks võimaluse hiljem mustal käia ruudule a7, mis võib olla strateegiliselt väga oluline. Ilmselt antud hetkel oleks parem käia e7, mis pööraks ümber ainult 1 piirinupu.
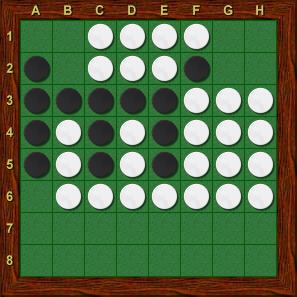
Joonis 24: Kas must tohiks käia a6 ??
Joonisel 24 on aga a6 parim käik. Kui valge vastaks b2 või g2, oleks järgmisel käigul kohe nurk musta oma, kui valge vastaks g1 (rohkem käike valgel poleks), siis must vastaks a7 ja valgel ei jääks muud üle kui nurk mustale anda (käies g2, b7 või g2). Sellel joonisel, käiku a6 kutsutakse täiuslikult vaikseks käiguks (perfectly quiet move) – ta ei pööra ühtegi piirinuppu ümber. Seega pole tähtis ainult kuhu mängija oma nupu asetab, vaid tähtis on ka see, millised nuppe ta selle käiguga ümber pöörab. Nende teadmistega on ka lihtsam mõista valge nõrkust joonisel 18: kogu piir on valge, ja mustal on suur valik käike, ning tal on täiuslikult vaikne käik ruudule e8, mis ei lisa mängu ühtegi musta piirinuppu. Valgel on aga raskused, kuna tal on palju piirinuppe, ja väga vähe võimalikke käike, mis on kõik halvad käigud.
Üks võimalus vähendada vastase mobiilsust on üritada ümber pöörata võimalikult vähe piirinuppe. On kasulikum omada pigem sisemisi nuppe kui piirinuppe. Sellist strateegiat kutsutakse keskvälja kontrollimise strateegiaks. Loomulikult pole see juhus, et joonisel 18 kõik mustad nupud on sisemised nupud.
Tempo, käikude ootamine
Vaatleme joonist 25. ülemine piir on jaotatud võrdselt valge ja musta mängija vahel.
Joonis 25: Musta käik.
On musta käik. Ta võib kaaluda käiku ülemisele küljele (e2, d2 ja c2 on mõistlikud käigud), kuid teine võimalus on lasta vastasel sinna enne käia ja suurendada seega vastase piirinuppude arvu seal. See on üks Othello paradoksaalsetest omadustest: on tihti ebasoodne käia, kuna sa pöörad ümber vastase nuppe ja riskeerid sellega, et annad vastasele uusi võimalikke käike. Nüüd, kuna must ei soovi käia ülemisse piirkonda, siis on tal ainuke võimalus käia alumisse piirkonda. Siin on tal 2 mõistlikku käiku: c8 ja d7. Kui must käib c8, siis valge, kes samuti ei taha ülemisse piirkonda käia, käib d7 (vt. Joonis 26), ja must peab ikkagi esimesena käima ülemisse piirkonda oma nupu. Aga kui must käiks d7, siis valgele oleks ainuke mõeldav käik c8, millele must saaks vastata käiguga b8 (vt. Joonis 27). Sellisel juhul öeldakse, et must võitis tempo alumises piirkonnas. Nüüd on valge see, kes peab käima esimesena ülemisse piirkonda.

Joonis 26: Musta käik (peale c8-d7)

Joonis 27: Mängu seis peale d7-c8-b8
Et saavutada tempo on seega vaja mängida nii, et oleks vastasest 1 käik rohkem, ja kui see käik tehtud, siis sundida vastast käima esimesena mujale (seeläbi sundida vastast suurendama tema piirinuppude arvu).
Joonisel 28 on järgmine näide, kuidas võita tempo piki mängulaua serva. Eesmärgiga vältida käimist ülemisse serva, peab must võitma tempo alumises servas. Kuidas seda teha? Kuidas valida c8 ja f8 vahel see õige käik? Mõni võib võibolla arvata, et need 2 käiku annavad sama tulemuse: c8-f8-g8 (vt. Joonis 29) või f8-c8-b8 (vt. Joonis 30).

Joonis 28: Musta käik

Joonis 29: Peale c8-f8-g8

Joonis 30: Peale f8-c8-b8.
Mõlemal juhul võidab must tempo ja sunnib valget käima esimesena mängulaua ülemisse serva. Kui aga vaatame lähemalt valge vastukäike mustale käigule, siis kui must käib c8, siis valgel on f8-st parem käik: ta saab käia hoopis g8! (vt. Joonis 31).
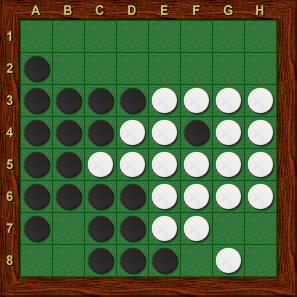
Joonis 31: Peale c8-g8.
Nüüd pole mustal enam ühtegi head käiku alumises servas (kui must käib f8, siis valge võtab kogu alumise serva käies b8) – seega pole must võitnud soovitud tempot. Seega seisus mis on joonisel 28, peab must käima f8, et võita tempo. Loomulikult on võimalik võita ka mitu tempot. Sellisel juhul on vastane veel halvemas olukorras kuna ta peab tegema mitu käiku enne kui mängija, kes võitis need tempod, on sunnitud suurendama oma piirinuppude arvu.
Joonis 32 on hea näide sellise olukorra kohta. Kui must käib a7 (vt. Joonis 33), siis on valge kohutavas seisus.
Loomulikult on valgel mitu mõistlikku käiku: g6, f2, e2 ja d2, aga tal pole võimalik käia kõiki nelja käiku. Täpsemalt on tal võimalus käia ainult 1 käik d2, e2 ja f2 hulgast, kuna nad kõik pööravad ümber sama musta nupu. Seega on valgel ainult 2 käiku. Teisest küljest, must saab võita tempo idaservas: ta saab käia a3, millele järgneb järgmisel käigul a2! Näiteks joonisel 34 on seis pärast käike e2-a3-g6-a2.
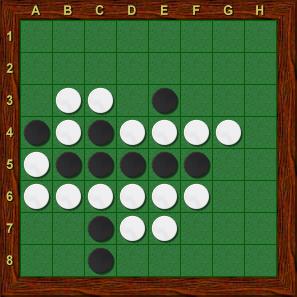
Joonis 32: Musta käik

Joonis 33: Peale musta käiku a7
Joonis 34: Peale a7-e2-a3-g6-a2.
Nüüd on valge sunnitud andma nurga a8 mustale. Tänu võidetud kolmele tempole idaservas, on valge sunnitud kaotama kõik musta piirinupud ülemises servas. Kahjuks võib aga meeleheitlik tempo võitmise üritus lõppeda kehvalt: mängija, kes üritab iga hinna eest tempot võita, tihtipeale leiab endal olevat halva nuppude paigutuse servas (tuletades meelde ka näiteks kiilude osa). Lisaks, nuppudel, mis asuvad servas on hiljem suur mõju mängu edasises käigus toimuvatele pööramistele: mängija on tihtipeale sunnitud pöörama ümber nuppe mitmes suunas iga käiguga. Joonisel 35, must on üritanud võita temposid, mängides alumisse- ja ülemisse serva. Nüüd kus ta peab mängima vasakus servas, on ta sunnitud pöörama nuppe ümber mitmes suunas, ja seega tekitama omale rohkem piirinuppe kui ta tahaks.

Joonis 35: Musta käik.
Hiilimine mööda servi
See arutelu viib meid ekstreemse tempovõitmise strateegiani. Seda nimetatakse mööda servi hiilimiseks. Üks kahest mängijast otsustab loobuda tsentri kontrollimisest ja hakkab korduvalt käima servadesse. Tulemus on tihti sarnane joonisel 36 olevaga.

Hiilimine võib aga lõppeda ka laastavalt. Kui vastasel õnnestub käia nii, et tal jääb alati erinevaid käiguvariante, siis avastab hiilinud mängija end olukorrast, kus nupud servades annavad tugeva negatiivse efekti mängu lõpuosas. Joonisel 38, mustal mängijal on ilmselt hiilimine ebaõnnestunud.

Seega võib öelda, et hiilimine on pigem lühiajaline strateegia (vastasel peavad kiirelt käigud otsa saama), põhjustades aga kahjulikke pikaajalise strateegia probleeme (ebaühtlased servad, nõrgad servad, mõju nuppude pööramisele). Lihtsalt öeldes: kui õnnestub, siis tuleb ilmselt võit, kui ebaõnnestub, siis on sellest väga raske välja tulla.
Paarsus
See äärmiselt tähtis fakt on ideaalseks lõpetuseks arutelule mobiilsuse kohta. Kui kumbki mängija käiku vahele ei jäta, siis on alati musta käigu ajal paaris arv tühje ruute laual ja paaritu arv, kui valge käib. Sellest võib järeldada, et valge käib üldjuhul mängus viimase käigu, ja see annab valgele väikese eelise kuna need nupud, mida ta viimase käiguga pöörab, on kindlalt stabiilsed nupud (need jäävad mängu lõppedes talle). Joonisel 39 peab must käima g8, millele järgneb valge käik h8 ja valge võidab mängu. Aga kui see oleks valge käik, siis ükskõik kumbale ruudule ta käiks (kas g8 või h8), teeks must viimase käigu ja võidaks mängu.

Paarsus annab eelise valgele. Samas aga on mustal võimalus see pöörata enda kasuks: nii kui keegi jätab käigu vahele, paarsus vahetub. Seega oleks mustale hea, kui mängu käigus jäetakse paaritu arv kordi käike vahele.
Üks hea võimalus mustal saavutada paarsus on tekitada paaritu piirkond, kuhu valge ei saa käia. Näiteks joonisel 41 valge ei saa käia ruudule g8, mis on üks paaritu piirkond (1 ruudune). Must ei tohiks ka sinna esialgu käia! Mustal oleks soovitatav käia teise paaritusse piirkonda, mis asub üleval paremas piirkonnas. Iga järgneva käiguga peakski must mängija vaatama, et pärast ta käiku jääks alles ainult paaris piirkonnad (v.a. See üks paaritu, kuhu vastane käia ei saa). Antud juhul peakski must käima ruudule g2.

Kui aga must oleks käinud kohe g8, siis oleks valge vastanud g1, mis oleks lauale jätnud 2 paaris piirkonda. Pärast käike g2-h1-a2-a1 võidaks valge 26-38.
Ebatasakaalus servad
Nüüd analüüsime ühte üsna sagedast kiilumise juhtumit. See näide on samuti tähtis kuna alati ei ole halb käia X-ruudule. Vaatame joonist 42.

Tuleb aga meeles pidada, et see ohverdus ei pruugi alati kasulik olla. Detailidesse süvenemata toome kolm näidet kus see ohverdus pole kasulik.

Joonisel 45 on natuke peenem situatsioon: mis juhtub, kui must ründab valge vasakut serva käies b7? Valge vastab a7! Kontrollides diagonaali f3-b7, mustal pole võimalik käia nurka ruudule a8 ja valge saab sinna käia oma järgmisel käigukorral tänu kiilule ruudul d8. Seega mustal on jällegi ebaõnnestunud plaan kiilutada oma nupp valgete nuppude vahele.

Lõksud
Me just nägime, et ebatasakaalus servade ründamine ei sunna vastast vahetama nurkasid. Lisaks, rünnatav mängija saab valida, kas võtta nurk või mitte. Järgnevalt näeme rohkem sunnitud serva lõksu, mille puhul on nurga saamine garanteeritud. Järgnev lõks kutsub tahtlikult vastast vahetama nurkasid. Kui see lõks on hästi paigutatud, siis pole vastasel mingit võimalust seda takistada.Lõksud koosnevad kahest etapist: Ründaja kõigepealt käib X-ruudule saavutades kontrolli diagonaali üle, seejärel ründab vastase nõrka serva ähvardades võtta nurk. Vastane ei saa võtta ähvardavat nuppu tagasi, kuna sel juhul ta pööraks ümber X-ruudul asuva nupu mille käis eelmisel käigul sinna ründaja. Joonisel 46 on selle kohta näide.



Kui valge tahab lõksu tegemiseks käia b7, siis must vastab c3 ja valge ei saa käia c8 peale, ning must võtab järgmise käiguga nurga a8. Selle tulemusena tekib alumisse serva paaris piirkond kuhu vahele enam kiilu lüüa ei saa.
